Вейвлет-сжатие на пальцах
31 Jan 2019Когда-то давно, ещё в феврале 2013 года я опубликовал две статьи на Хабре, посвящённые вейвлет-сжатию. Моей целью было максимально просто и доступно, на уровне школы или первого курса рассказать о вейвлетах. Во второй, практической части многое нужно уже исправить и переработать. А вот первая часть всё ещё годится в качестве начального введения. Привожу её с исправлениями и дополнениями.
Введение
Если вы когда-нибудь интересовались сжатием изображений, то, возможно, слышали о вейвлетах. Они используются, например, в формате сжатия JPEG2000, который превосходит по качеству своего предка — JPEG. Или в популярном формате для хранения сканированных документов DjVu.
Литература о теории вейвлетов пестрит интегралами и терминами из теории обработки сигналов. Но на самом деле, понять, чем же хороши вейвлеты можно и не углубляясь в сложную местами (хоть и интересную) теорию.
Попробуем на простых примерах разобраться, как вообще сжимаются изображения и как для этого применить вейвлета. Предполагается, что читатель знаком с основами линейной алгебры, не боится слов вектор и матрица, а также умеет их перемножать.
Сжатие изображений
Упрощённо, изображение представляют собой таблицу, в ячейках которой хранятся цвета каждого пикселя. Если мы работаем с чёрно-белым (или, точнее, серым) изображением, то вместо цвета в ячейки помещают значения яркости из отрезка \([0, 1]\). При этом 0 соответствует чёрному цвету, 1 — белому. Но с дробями работать неудобно, поэтому часто значения яркости берут целыми из диапазона от 0 до 255. Тогда каждое значение будет занимать ровно 1 байт.
Даже небольшие изображения требуют много памяти для хранения. Так, если мы кодируем яркость каждого пикселя одним байтом, то изображение одного кадра формата FullHD (1920×1080) займёт почти два мегабайта. Представьте, сколько памяти потребуется для хранения полуторачасового фильма!
Поэтому изображения стремятся сжать. То есть закодировать таким образом, чтобы памяти для хранения требовалось меньше. А во время просмотра мы декодируем записанные в память данные и получаем исходный кадр. Но это лишь в идеале.
Существует много алгоритмов сжатия данных. О их количестве можно судить по форматам, поддерживаемым современными архиваторами: ZIP, 7zip, RAR, gzip, bzip2 и так далее. Неудивительно, что благодаря активной работе учёных и программистов в настоящее время степень сжатия данных вплотную подошла к теоретическому пределу.
Плохая новость в том, что для изображения этот теоретический предел не так уж и велик. Попробуйте сохранить фотографию (особенно с большим количеством мелких деталей) в формате PNG — размер получившегося файла может вас расстроить.
Это происходит из-за того, что в изображениях из реального мира (фотографиях, например) значения яркости редко бывают одинаковыми даже у соседних пикселей. Всегда есть мельчайшие колебания, которые неуловимы человеческим глазом, но которые алгоритм сжатия честно пытается учесть.
Алгоритмы сжатия «любят», когда в данных есть закономерность. Лучше всего сжимаются длинные последовательности нулей (закономерность тут очевидна). В самом деле, вместо того, чтобы записывать в память 100 нулей, можно записать просто число 100 (конечно, с пометкой, что это именно количество нулей). Декодирующая программа «поймёт», что имелись в виду нули и воспроизведёт их.
Однако если в нашей последовательности в середине вдруг окажется единица, то одним числом 100 ограничится не удастся.
Но зачем кодировать абсолютно все детали? Ведь когда мы смотрим на фотографию, нам важен общий рисунок, а незначительные колебания яркости мы и не заметим. А значит, при кодировании мы можем немного изменить изображение так, чтобы оно хорошо кодировалось. При этом степень сжатия сразу вырастет. Правда, декодированное изображение будет незначительно отличаться от исходного, но кто заметит?
Преобразование Хаара
Итак, наша цель — преобразовать изображение так, чтобы оно хорошо сжималось классическими алгоритмами. Подумаем, как нужно изменить его, чтобы получить длинные цепочки нулей.
У «реальных» изображений, таких как фотографии, есть одна особенность — яркость соседних пикселей обычно отличается на небольшую величину. В самом деле, в мире редко можно увидеть резкие, контрастные перепады яркости. А если они и есть, то занимают лишь малую часть изображения.
Давайте рассмотрим конкретный пример. В цифровой обработке изображений часто в качестве тестового изображения используют фотографию Лены Сёдерберг. Её часто можно увидеть в статьях.

Чтобы пока не углубляться в детали кодирования цветных изображений, для каждого пикселя оставим только значения яркости.

Рассмотрим яркости первой строки пикселей.
154, 155, 156, 157, 157, 157, 158, 156
Видно, что соседние числа очень близки. Чтобы получить желаемые нули или хотя бы что-то близкое к ним, можно закодировать отдельно первое число, а потом рассматривать лишь отличия каждого числа от предыдущего.
Получаем:
154, 1, 1, 1, 0, 0, 1, -2.
Уже лучше! Такой метод в самом деле используется и называется дельта-кодированием. Но у него есть серьёзный недостаток — он нелокальный. То есть нельзя взять кусочек последовательности и узнать, какие именно яркости в нём закодированы без декодирования всех значений перед этим кусочком.
Попробуем поступить иначе. Не будем пытаться сразу получить хорошую последовательность, попробуем улучшить её хотя бы немного.
Для этого разобьём все числа на пары и найдём полусуммы и полуразности значений в каждой из них.
(154, 155), (156, 157), (157, 157), (158, 156)
(154.5, 0.5), (156.5, 0.5), (157, 0.0), (157, -1.0)
Почему именно полусуммы и полуразности? А всё очень просто! Полусумма — это среднее значение яркости пары пикселей. А полуразность несёт в себе информацию об отличиях между значениями в паре. Очевидно, зная полусумму \(a\) и полуразность \(d\) можно найти и сами значения: первое значение в паре равно \(a - d\), второе значение в паре равно \(a + d\).
Это преобразование было предложено в 1909 году Альфредом Хааром и носит его имя.
А где же сжатие?
Полученные числа можно перегруппировать по принципу «мухи отдельно, котлеты отдельно», разделив полусуммы и полуразности:
154.5, 156.5, 157, 157; 0.5, 0.5, 0.0, -1.0.
Числа во второй половине последовательности как правило будут небольшими (то, что они не целые, пусть пока не смущает). Почему так?
Как мы уже выяснили раньше, в реальных изображениях соседние пиксели редко отличаются друг от друга значительно. Если значение одного велико, то и другого велико. В таких случаях говорят, что соседние пиксели коррелированы.
Запишем яркости всех пикселей построчно в виде одной длинной цепочки, рассмотрим пары соседних пикселей и каждую пару представим на графике точкой.
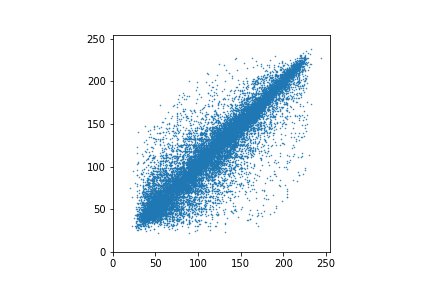
Точки выстраиваются близко к диагонали, что означает, что яркости соседних пикселей примерно одинаковы. И так практически во всех реальных изображениях. Верхний левый и нижний правый углы изображения практически всегда пусты.
Ещё лучше это видно на графике, построенном по первым 2048 пикселям — они соответствуют верхним строкам изображения, где нет резких переходов.
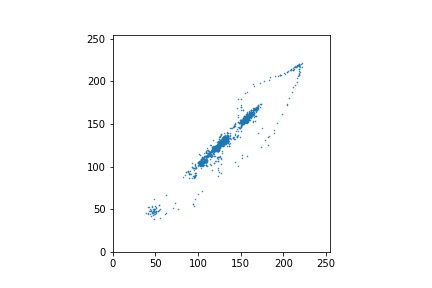
А теперь рассмотрим график, точками в котором будут полусуммы и полуразности.
Это для всех пикселей.
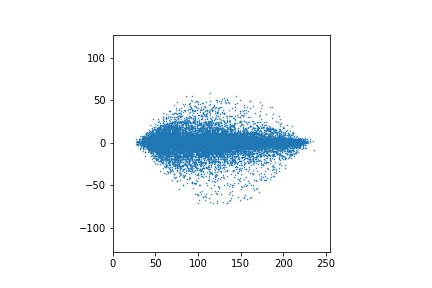
А это для первых 2048 значений.
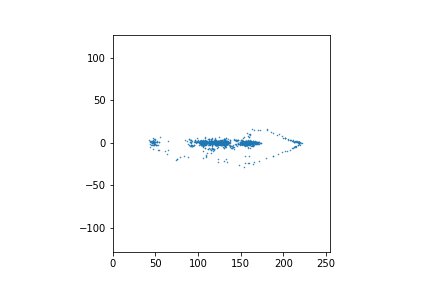
Видно, что полуразности находятся в более узком диапазоне значений. А это значит, что на них можно потратить меньше одного байта (правда, с небольшой потерей точности). Какое-никакое, а сжатие.
Применим математику!
Попробуем записать математические выражения, описывающие преобразование Хаара.
Итак, у нас была пара пикселей (вектор) \(\begin{pmatrix} x \\ y \end{pmatrix}\), а мы хотим получить пару \(\begin{pmatrix} \frac{y+x}2 \\ \frac{y-x}2 \end{pmatrix}\).
Такое преобразование описывается матрицей
\[\begin{pmatrix} \phantom{-}\frac12 & \frac12 \\ -\frac12 & \frac12 \end{pmatrix}.\]В самом деле
\[\begin{pmatrix} \phantom{-}\frac12 & \frac12 \\ -\frac12 & \frac12 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} \frac{y+x}2 \\ \frac{y-x}2 \end{pmatrix},\]что нам и требовалось.
Внимательный читатель наверняка заметил, что рисунки из точек на двух последних графиках одинаковы. Разница лишь в повороте на угол в 45°.
В математике повороты, отражения и растяжения называются аффинными преобразованиями и описываются как раз при помощи умножения матрицы на вектор. Что мы и получили выше. То есть, преобразование Хаара — это просто поворот точек таким образом, чтобы их можно было удобно и компактно закодировать.
Правда, тут есть один нюанс. При аффинных преобразованиях может меняться площадь фигуры. Не то, чтобы это было плохо, но как-то неаккуратненько. Как известно, коэффициент изменения площади равен определителю матрицы. Посмотрим, какой он для преобразования Хаара.
\[\det\begin{pmatrix} \phantom{-}\frac12 & \frac12 \\ -\frac12 & \frac12 \end{pmatrix} = \frac12\cdot\frac12-\left(-\frac12\cdot\frac12\right) = \frac12\]Для того, чтобы определитель стал равен единице достаточно умножить каждый элемент матрицы на \(\sqrt2\). На угол поворота (а значит, и на «сжимающую способность» преобразования) умножение на константу не повлияет.
Получаем в итоге матрицу
\[H = \begin{pmatrix} \phantom{-}\frac1{\sqrt2} & \frac1{\sqrt2} \\ -\frac1{\sqrt2} & \frac1{\sqrt2} \end{pmatrix}.\]А как декодировать?
Как известно, если у матрицы определитель не равен нулю, то для неё существует обратная матрица, «отменяющая» её действие. Если мы найдём обратную матрицу для \(H\), то декодирование будет заключаться просто в умножении векторов с полусуммами и полуразностями на неё:
\[\begin{pmatrix} x \\ y \end{pmatrix} H^{-1} = \begin{pmatrix} s \\ d \end{pmatrix}.\]Вообще говоря, поиск обратной матрицы — не такая простая задача. Но, может, удастся как-то эту задачу упростить?
Рассмотрим поближе нашу матрицу. Она состоит из двух вектор-строк: \(\left(\frac1{\sqrt2},\frac1{\sqrt2}\right)\) и \(\left(-\frac1{\sqrt2},\frac1{\sqrt2}\right)\). Назовём их \(v_1\) и \(v_2\).
Они обладают интересными свойствами.
Во-первых, их длины равны 1, то есть
\[v_1 v_1^T = v_2 v_2^T = 1.\]Здесь буква \(T\) означает транспонирование — обмен строк и столбцов местами. Умножение вектор-строки на транспонированную вектор-строку (то есть, вектор-столбец) — это обычное скалярное произведение.
Во-вторых, они ортогональны, то есть
\[v_1 v_2^T = v_2 v_1^T = 0.\]Матрица, строки которой обладают указанными свойствами называется ортогональной. Чрезвычайно важным свойством таких матриц является то, что обратную матрицу для них можно получить простым транспонированием.
\[H^{-1} = H^T = \begin{pmatrix} \phantom{-}\frac12 & \frac12 \\ -\frac12 & \frac12 \end{pmatrix}^T = \begin{pmatrix} \frac12 & -\frac12 \\ \frac12 & \phantom{-}\frac12 \end{pmatrix}.\]В справедливости этого выражения можно убедиться умножив \(H\) на обратную матрицу. На диагонали мы получим скалярные произведения вектор-строк на самих себя, то есть 1. А вне диагоналей — скалярные произведения вектор-строк друг на друга, то есть 0. В итоге произведение будет равно единичной матрице
\[\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}.\]А единичная матрица — это отсутствие преобразования, так как она не меняет вектор.
Мы любим ортогональные матрицы!
Увеличиваем число точек
Всё сказанное хорошо работает для двух точек. Но что делать, если точек больше?
В этом случае тоже можно описать преобразование матрицей, но большей по размеру. Диагональ этой матрицы будет состоять из матриц H, таким образом в векторе исходных значений будут выбираться пары, к которым независимо будет применяться преобразование Хаара.
\[\begin{pmatrix} \phantom{-}\frac1{\sqrt{2}} & \frac1{\sqrt{2}} &&& \\ -\frac1{\sqrt{2}} & \frac1{\sqrt{2}} &&& \\ && \phantom{-}\frac1{\sqrt{2}} & \frac1{\sqrt{2}} & \\ && -\frac1{\sqrt{2}} & \frac1{\sqrt{2}} & \\ &&&& \ddots \end{pmatrix}\](Договоримся, что в пустых ячейках стоят нули.)
То есть, исходный вектор просто обрабатывается независимо по парам.
Фильтры
Итак, когда мы знаем, как выполнять преобразование Хаара, попробуем разобраться с тем, что же оно нам даёт.
Полученные «полусуммы» (из-за того, что делим не на 2, приходится использовать кавычки) — это, как мы уже выяснили, средние значения в парах пикселей. То есть, фактически, значения полусумм — это уменьшенная копия исходного изображения! Уменьшенная потому, что полусумм в два раза меньше, чем исходных пикселей.
Но что такое разности?
Полусуммы усредняют значения яркостей, то есть «убирают» случайные всплески значений. Можно считать, что это некоторый частотный фильтр, убирающий высокочастотную компоненту изображения.
Фильтр, пропускающий низкие частоты, называется фильтром низких частот.
Аналогично, разности «выделяют» среди значений межпиксельные «всплески» и устраняют константную составляющую. То есть, они «убирают» низкие частоты.
Таким образом, преобразование Хаара — это пара фильтров, разделяющих сигнал на низкочастотную и высокочастотную составляющие. Чтобы получить исходный сигнал, нужно просто снова объединить эти составляющие.
Что нам это даёт? Пусть у нас есть фотография-портрет. Низкочастотная составляющая несёт в себе информацию об общей форме лица, о плавных перепадах яркости. Высокочастотная — это шум и мелкие детали.
Обычно, когда мы смотрим на портрет, нас больше интересует низкочастотная составляющая, а значит при сжатии часть высокочастотных данных можно отбросить. Тем более, что, как мы выяснили, она обычно имеет меньшие значения, а значит более компактно кодируется.
Степень сжатия можно увеличить, применяя преобразование Хаара многократно. В самом деле, высокочастотная составляющая — это всего лишь половина от всего набора чисел. Но что мешает применить нашу процедуру ещё раз к низкочастотным данным? После повторного применения, высокочастотная информация будет занимать уже 75 %.
Сжатие изображения
Хоть мы пока и говорили об одномерных цепочках чисел, этот подход хорошо применим и для двумерных данных. Чтобы выполнить двумерное преобразование Хаара (или аналогичное ему), нужно лишь выполнить его для каждой строки и для каждого столбца.
Для работы с цветными изображениями можно просто обрабатывать три цветовые компоненты независимо. Для сжатия чаше используют не цветовое пространство \(RGB\) (когда цвет кодируется значениями красной, зеленой и синей компонент), а \(Y'C_BC_R\) или подобные. В них первая компонента — яркость, а остальные две отвечают за цвет. Глаз человека более чувствителен к изменению яркости, а значит цвет можно сжать сильнее с бо́льшими потерями без заметного снижения качества.
Если применить этот подход к цветной фотографии, то получится 4 набора чисел — три с высокочастотными составляющими и один с низкочастотными.

Никто не мешает применить преобразование повторно к уменьшенному низкочастотному блоку.

Или вовсе многократно пока позволяют размеры получающегося низкочастотного блока.

Черные области соответствуют низкой яркости, то есть значениям, близким к нулю. Как показывает практика, если значение достаточно мало, то его можно округлить или вообще обнулить без особого ущерба для декодированного рисунка.
Этот процесс называется квантованием. И именно на этом этапе Происходит потеря части информации. (К слову, такой же подход используется в JPEG, только там вместо преобразования Хаара используется дискретное косинус-преобразование. Это преобразование, на самом деле, — тоже разновидность умножения на матрицу.) Меняя число обнуляемых коэффициентов, можно регулировать степень сжатия!
Конечно, если обнулить слишком много, то искажения станут видны на глаз. Во всём нужна мера!
После всех этих действий у нас останется матрица, содержащая много нулей. Её можно записать построчно в файл и сжать каким-то архиватором. Например, тем же 7Z. Результат будет неплох.
Декодирование производится в обратном порядке: распаковываем архив, применяем обратное преобразование Хаара и записываем декодированную картинку в файл. Вуаля!
Где эффективно преобразование Хаара?
Когда преобразование Хаара будет давать наилучший результат? Очевидно, когда мы получим много нулей, то есть, когда изображение содержит длинные участки одинаковых значений яркости. Тогда все разности обнулятся. Это может быть, например, рентгеновский снимок, отсканированный документ.
Говорят, что преобразование Хаара устраняет константную составляющую, то есть переводит константы в нули. Это ещё называют устранением или обнулением так называемых моментов нулевого порядка.
Но всё же в реальных фотографиях областей с одинаковой яркостью не так много. Попробуем усовершенствовать преобразование, чтобы оно обнуляло ещё и линейную составляющую. Иными словами, если значения яркости будут увеличивать линейно, то они тоже обнулятся.
Эту задачу и более сложные (устранение моментов более высоких порядков) решила Ингрид Добеши — один из создателей теории вейвлетов.
Преобразование Добеши
Для нашего усовершенствованного преобразования уже будет мало двух точек. Поэтому будем брать по четыре значения, смещаясь каждый раз на два.
То есть, если исходная последовательность имеет вид
\[1, 2, 3, 4, 5, 6, \dots, N-1, N,\]то будем брать четвёрки с шагом 2:
\[(1, 2, 3, 4), (3, 4, 5, 6), \dots\]Последняя четвёрка «кусает последовательность за хвост»:
\[(N-1, N, 1, 2).\]Дело в том, что каждой четвёрке мы ставим в соответствие пару чисел. Если в исходной последовательности всего 6 чисел, то не выходя за край мы сможем получить только 4 числа. По ним исходные 6 не восстановить.
Чтобы выйти за край нужно сперва договориться, что за ним находится. Можно считать, что после последнего элемента последовательность начинается сначала (как мы только что и проделали подставив элементы 1 и 2). А можно просто подставить нули. Правильный выбор соглашения об обработке границ влияет на качество их кодирования. Но так как границы составляют лишь малую часть изображения, то этот вопрос не такой уж и сильно влияет на общий принцип кодирования.
Точно так же попробуем построить два фильтра: высокочастотный и низкочастотный. Каждую четвёрку будем заменять на два числа. Так как четвёрки перекрываются, то количество значений после преобразования не изменится.
Для того, чтобы было удобно считать обратную матрицу потребуем также ортогональности преобразования. Тогда поиск обратной матрицы сведётся к транспонированию
Пусть значения яркостей в четвёрке равны \(x, y, z, t.\) Тогда первый фильтр запишем в виде
\[a = c_1x + c_2y + c_3z + c_4z.\]Четыре коэффициента, образующих вектор-строку матрицы преобразования, пока нам неизвестны.
Чтобы вектор-строка коэффициентов второго фильтра был ортогонален первому, возьмём те же коэффициенты но переставим их и поменяем знаки:
\[d = c_4x - c_3y + c_2z - c_1t.\]Матрица преобразования будет иметь вид
\[\begin{pmatrix} c_1 & \phantom{-}c_2 & c_3 & \phantom{-}c_4 &&& \\ c_4 & -c_3 & c_2 & -c_1 &&& \\ && c_1 & \phantom{-}c_2 & c_3 & \phantom{-}c_4 & \\ && c_4 & -c_3 & c_2 & -c_1 & \\ &&&&&& \ddots \end{pmatrix}.\]Требование ортогональности выполняется для первой и второй строк автоматически. Потребуем, чтобы строки 1 и 3 тоже были ортогональны, для этого их скалярное произведение должно быть равно 0:
\[c_3c_1 + c_4c_2 = 0.\]Векторы должны иметь единичную длину (иначе определитель не будет единичным):
\[c_1^2 + c_2^2 + c_3^2 + c_4^2 = 1.\]Преобразование должно обнулять цепочку одинаковых значений (например, \((1, 1, 1, 1)\)):
\[1\cdot c_4 - 1\cdot c_3 + 1\cdot c_2 - 1\cdot c_1 = 0.\]Преобразование должно обнулять цепочку линейно растущих значений (например, \((1, 2, 3, 4)\)):
\[1\cdot c_4 - 2\cdot c_3 + 3\cdot c_2 - 4\cdot c_1 = 0.\]Кстати, если обнуляется эта четвёрка, то будут обнуляться и любые другие линейно растущие или линейно убывающие. В этом легко убедиться, записав соответствующее уравнение и разделив все коэффициенты на первый множитель.
Получили 4 уравнения, связывающие коэффициенты: \(\begin{cases} c_3c_1 + c_4c_2 = 0,\\ c_1^2 + c_2^2 + c_3^2 + c_4^2 = 1,\\ c_4 - c_3 + c_2 - c_1 = 0,\\ c_4 - 2c_3 + 3c_2 - 4c_1 = 0. \end{cases}\)
Система нелинейная, и чтобы найти решение нужно немного повозиться или воспользоваться какой-нибудь компьютерной программой.
Решение (одно из) имеет вид:
\[\begin{cases} c_1 = \frac{1+\sqrt3}{4\sqrt2},\\ c_2 = \frac{3+\sqrt3}{4\sqrt2},\\ c_3 = \frac{3-\sqrt3}{4\sqrt2},\\ c_4 = \frac{1-\sqrt3}{4\sqrt2}.\\ \end{cases}\]Подставив коэффициенты в матрицу, получаем искомое преобразования. После его применения к фотографиям получим больше нулей и малых коэффициентов, чем после преобразования Хаара, что позволит сжать изображение сильнее.
Другая приятная особенность — артефакты после квантования будут не так заметны.
Это преобразование получило название вейвлета D4 (читателю предлагается самостоятельно разгадать тайну этого буквенно-цифрового названия).
О нормировке
Если посмотреть коэффициенты в википедии, то можно заметить, что они отличаются от тех, что получили мы. Дело в том, что в теории вейвлетов обычно используется нормировка не на 1, а на 2. То есть, произведение матрицы преобразования и матрицы обратного преобразования должно быть равно удвоенной единичной матрице, а не просто единичной.
Если заменить в правой части второго уравнения 1 на 2 и решить систему, то получим те же коэффициенты, что и в Википедии.
А, скажем, в статье P. Getreuer Filter Coefficients to Popular Wavelets, в которой приводятся коэффициенты для распространённых вейвлетов, значения те же, что и у нас.
Сравнение вейвлетов Хаара и Добеши
Как и в случае вейвлета Хаара, вейвлет D4 можно применить к цветному изображению.

Мы, конечно, можем не остановиться на этом, и потребовать устранения параболической составляющей (момент 2-го порядка) и так далее. В результате получим вейвлеты D6, D8 и другие.
Для наглядности сравним вейвлеты Хаара (слева) и Добеши D8 (справа).

Если приглядеться, то видно, что после преобразования Добеши в высокочастотной области меньше деталей. Например, нет вертикальных линий, соответствующим контрастным переходам на фоне. Это значит, что значения в этих областях ближе к нулю и их проще сжать.
Добеши предложила весьма интересный способ получения коэффициентов этих преобразований, но увы, это уже выходит за рамки нашей статьи. Мы не пытаемся построить теорию вейвлетов, а лишь выводим их из простых практических соображений.
Домашнее задание
Чтобы окончательно разобраться с основами, предлагаю написать на вашем любимом языке программу, которая открывает изображение, выполняет преобразование Хаара (или даже D4), квантует результат, а потом сохраняет результат в файл. Попробуйте сжать этот файл своим любимым архиватором. Хорошо сжимается?
Попробуйте выполнить обратное преобразование. Как вы объясните характер артефактов на изображении?
Заключение
Итак, мы кратко рассмотрели основные идеи дискретного вейвлет-преобразования.
Конечно, в этой статье не были рассмотрены очень многие интересные математические детали и практические применения вейвлет-преобразований. На практике применяются более сложные, но и более эффективные подходы. Разумеется, это только самые основы. И на самом деле вейвлеты конструируются не так, как описано. Но многое сложно объяснить не повышая градус матана. Надеюсь, что у читателя после прочтения этой статьи появилось общее представление о том, как используются вейвлеты в области сжатия изображений.
Литература
См. также мою статью «Схема лифтинга».
Есть много довольно неплохих книжек, которые дают более глубокое представление о вейвлетах. Начать рекомендую со следующих:
- Уэлстид С. Фракталы и вейвлеты для сжатия изображений в действии. — М.: Триумф, 2003.
- Штарк Г.-Г. Применение вейвлетов для ЦОС. — М.: Техносфера, 2007.
- Протасов В. Всплески Ингрид Добеши.
